Answer:
k = 13.5
xy = 13.5
Explanation:
Inverse variation states:
If

then, the equation is in the form of:
 where, k si the constant of variation.
where, k si the constant of variation.
or xy = k ......[1]
As per the statement:
Given: y = 4.5 and x = 3
Using the definition of inverse variation, solve for k;
Substitute the given values in [1] we have;

⇒13.5 = k
then, we get equation:
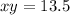
Therefore, the constant of variation(k) is, 13.5 and an equation for the inverse variation is, xy = 13.5