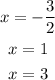Question

Solve the equation: 2x^3-5x^2-6x+9=0 given that x=1 is a zero

Answer 1

The given function

`2x^3+5x^2-6x+9=0`

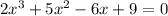
Since x = 1 is one of its zeroes, then we will use it to find the other zeroes

`\begin{gathered} x=1 \\ x-1=1-1 \\ x-1=0 \end{gathered}`

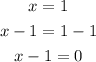
The factor is x - 1

Use the long division to find the other factors

`(2x^3-5x^2-6x+9)/(x-1)`

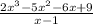
Divide 2x^3 by x, then multiply the answer by (x - 1)

`\begin{gathered} (2x^3)/(x)=2x^2 \\ 2x^2(x-1)=2x^3-2x^2 \end{gathered}`

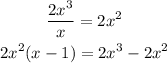
Subtract the product from the original equation

`\begin{gathered} 2x^3-5x^2-6x+9-(2x^3-2x^2)= \\ (2x^3-2x^3)+(-5x^2+2x^2)-6x+9= \\ 0-3x^2-6x+9 \\ (2x^3-5x^2-6x+9)/(x-1)=2x^2+(-3x^2-6x+9)/(x-1) \end{gathered}`

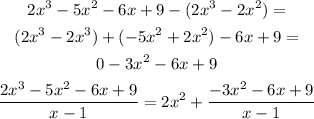
Now, divide -3x^2 by x, then multiply the answer by (x - 1)

`\begin{gathered} -(3x^2)/(x)=-3x \\ -3x(x-1)=-3x^2+3x \end{gathered}`

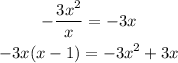
Subtract it from the denominator of the fraction

`\begin{gathered} (-3x^2-6x+9)-(-3x^2+3x)= \\ (-3x^2+3x^2)+(-6x-3x)+9= \\ 0-9x+9 \\ (2x^2-5x^2-6x+9)/(x-1)=2x^2-3x+(-9x+9)/(x-1) \end{gathered}`

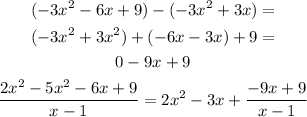
Divide -9x by x and multiply the answer by (x - 1)

`\begin{gathered} (-9x)/(x)=-9 \\ -9(x-1)=-9x+9 \end{gathered}`

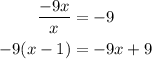
Subtract it from the numerator

`\begin{gathered} -9x+9-(-9x+9)= \\ (-9x+9x)+(9-9)= \\ 0+0 \\ (2x^3-5x^2-6x+9)/(x-1)=2x^2-3x-9 \end{gathered}`

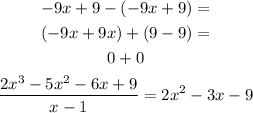
Then we will factor this trinomial into 2 factors

`\begin{gathered} 2x^2=(2x)(x) \\ -9=(-3)(3) \\ (2x)(-3)+(x)(3)=-6x+3x=-3x\rightarrow middle\text{ term} \\ 2x^2-3x^2-9=(2x+3)(x-3) \end{gathered}`

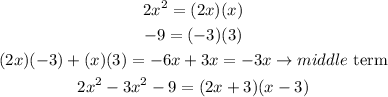
Equate each factor by 0 to find the other zeroes of the equation

`\begin{gathered} 2x+3=0 \\ 2x+3-3=0-3 \\ 2x=-3 \\ (2x)/(2)=(-3)/(2) \\ x=-(3)/(2) \end{gathered}`
`\begin{gathered} x-3=0 \\ x-3+3=0+3 \\ x=3 \end{gathered}`

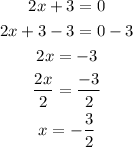
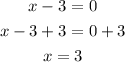
The zeroes of the equations are 1, 3, -3/2

The solutions of the equations are

`\begin{gathered} x=-(3)/(2) \\ x=1 \\ x=3 \end{gathered}`