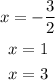The given function
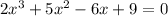
Since x = 1 is one of its zeroes, then we will use it to find the other zeroes

The factor is x - 1
Use the long division to find the other factors
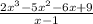
Divide 2x^3 by x, then multiply the answer by (x - 1)

Subtract the product from the original equation
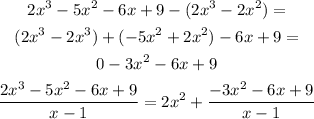
Now, divide -3x^2 by x, then multiply the answer by (x - 1)
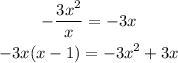
Subtract it from the denominator of the fraction
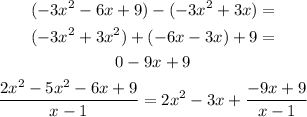
Divide -9x by x and multiply the answer by (x - 1)
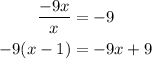
Subtract it from the numerator
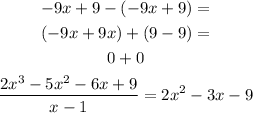
Then we will factor this trinomial into 2 factors
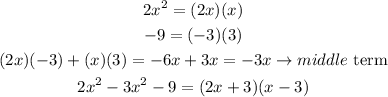
Equate each factor by 0 to find the other zeroes of the equation
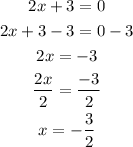

The zeroes of the equations are 1, 3, -3/2
The solutions of the equations are