If a hyperbola is centered at the origin and has vertex and focus on the x-axis, then its equation is
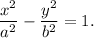
1. The vertex A of hyperbola has coordinates (-6,0), then the distance from the origin (center of the hyperbola) to the vertex is
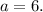
2. The focus F has coordinates (10,0), then the distance from the origin to the focus is
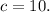
3. Find b, using formula
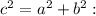
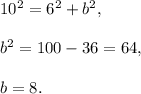
4. The equation of the hyperbola is
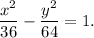
5. The directrices' equations are
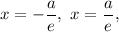
where
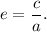
In your case,
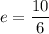
and directrices' equations are
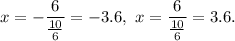
Answer: x=-3.6, x=3.6, correct choice is C