Answer:
discriminant of the quadratic equation is -16, The resulting number is less than zero so there are no real number solutions.
Explanation:
Given : he quadratic equation −1 = 5x² −2x.
To find : What is the value of the discriminant .
Solution : We have given that −1 = 5x² −2x.
−1 = 5x² −2x.
On adding by 1 both sides
0 = 5x² −2x +1
On switching sides
5x² −2x +1 = 0
Compare it standard form of quadratic equation ax² +bx +c = 0.
Here, a = 5, b= -2, c = 1
By Discriminant formula:
D =
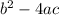
Substituting the values
D =
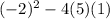 .
.
D = 4 - 20
D = -16.
Therefore, discriminant of the quadratic equation is -16, The resulting number is less than zero so there are no real number solutions.