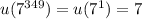Let
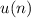
be the units digits of the number

.
Clearly,
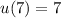
.
Since
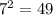
, we have

.
Next,
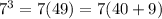
, so only the product

will contribute to the value of
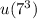
; indeed,
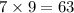
, so
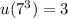
.
Next,
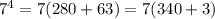
, and
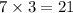
, so by the same reasoning as before we have

.
Continuing in this pattern, we find that
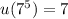
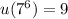
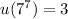
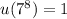
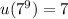
and so on, with the repeating pattern of

with a period of 4. This means that
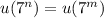
, where
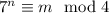
.
Now,

, i.e.
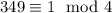
, so