Answer:
The area of the two-dimensional cross section that is parallel to face ABC. that is Area of Δ DEF = 84 ft²
Step-by-step explanation:
Given : A triangular prism with some side measurement.
We have to find the area of the two-dimensional cross section that is parallel to face ABC.
Since, the cross section that is parallel to face ABC.
Since, face parallel to ABC is DEF .
And DEF is a triangle with ∠ E = 90°
So, Area of right angled triangle

Base = 24 ft
and height is 7 ft
So, Area of Δ DEF =
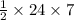
Simplify , we have,
Area of Δ DEF = 84 ft²
Thus, The area of the two-dimensional cross section that is parallel to face ABC. that is Area of Δ DEF = 84 ft²