Answer:
The answer is:
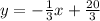
Explanation:
The slope of line y = 3x - 3 is k = 3, so the negative reciprocal is given by -1/k. Therefore the slope for the perpendicular equation is -1/3.
Now, the perpendicular equation passes through the point x = -7 y = 9, so you need to find b:
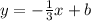 // replace y = 9 and x = -7
// replace y = 9 and x = -7
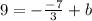 // substract 7/3 in both sides
// substract 7/3 in both sides
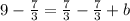 // solve
// solve
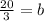
Replace b in the equation:
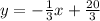
See the attachment.