Question

Suppose that 5 identical red wooden blocks and 6 identical white wooden blocks are to be​ stacked, one on top of​ another, to form one tall tower of blocks. How many different colour patterns can​ result?

Answer 1

462

Explanation:

Firstly, we will calculate the number of ways we can arrange total number of wooden blocks. Lets say each of them are independent, so altogether we have
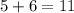`5+6=11` blocks. And number of ways to arrange 11 blocks would simply be:
`11!`.

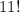Now, we need to figure out the number of ways 5 red wooden blocks can be arranged, it is
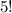`5!` and the number of ways 6 white wooden blocks can be arranged is
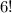`6!`. These are the ways they can be arranged in themselves.

So, we can now find how many different colour patterns can result by:

`\frac{\text {ways all blocks can be stacked}}{\text{ways red blocks can be stacked} * \text{ways white blocks can be stacked}}`

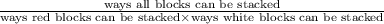
So in this case it is:

`=(11!)/(5! * 6!) =462`

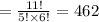
Therefore, there could be 462 colour patterns.