Question

Compute the permutations and combinations. How many two-digit, positive integers can be formed from the digits 1, 3, 5, and 9, if no digit is repeated?

a. 12
b. 16
c. 24

Answer 1

the awnser will be a

Answer 2

Answer: The correct option is (a) 12.

Step-by-step explanation: We are given to find the number of two-digit positive integers that can be formed from the digits 1, 3, 5, and 9, if no digit is repeated.

Here, we have 4 digits, out of which we have to choose the digits for the two places.

For first place, we have 4 options.

Since no digit is repeated, so we have 3 options for the second place.

Therefore,

the number of two-digit positive integers that can be formed from the digits 1, 3, 5, and 9, if no digit is repeated is given by the permutation of 4 digits taken 2 at a time.

Thus, the total number of two-digit positive integers will be

`n=^4P_2=(4!)/((4-2)!)=(4!)/(2!)=(4*3*2!)/(2!)=12.`

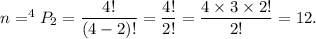
Option (a) is CORRECT.