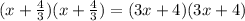Answer: Option 2 is correct (3x+4)(3x+4)
Step-by-step explanation:
we have general form of quadratic equation
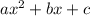
Given quadratic is
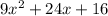
We will use the formula for discriminant which is
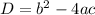
On comparing the given quadratic equation with the general quadratic equation we get a=9 , b=24,c=16
substituting the values in the formula for discriminant we will get
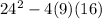 =0
=0
Now, to find x we have formula
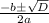
D=0 , b=24, c=16 substituting the values we will get
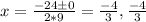
factors are