Question

Find a particular solution to
`x^(2) ( d^(2)y )/(d x^(2) ) +6x (dy)/(dx) +4y= x^(2) sin(x)` in x>0

Answer 1

`y=x^r`

`\implies r(r-1)x^r+6rx^r+4x^r=0`

`\implies r^2+5r+4=(r+1)(r+4)=0`

`\implies r=-1,r=-4`

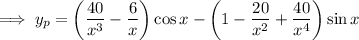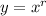
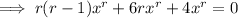
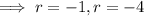
so the characteristic solution is


`y_c=\frac{C_1}x+(C_2)/(x^4)`

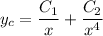
As a guess for the particular solution, let's back up a bit. The reason the choice of
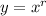
`y=x^r` works for the characteristic solution is that, in the background, we're employing the substitution
`t=\ln x`, so that
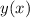
`y(x)` is getting replaced with a new function
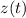
`z(t)`. Differentiating yields


`(\mathrm dy)/(\mathrm dx)=\frac1x(\mathrm dz)/(\mathrm dt)`

`(\mathrm d^2y)/(\mathrm dx^2)=\frac1{x^2}\left((\mathrm d^2z)/(\mathrm dt^2)-(\mathrm dz)/(\mathrm dt)\right)`

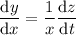
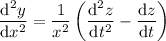
Now the ODE in terms of
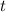
`t` is linear with constant coefficients, since the coefficients
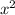
`x^2` and
`x` will cancel, resulting in the ODE


`(\mathrm d^2z)/(\mathrm dt^2)+5(\mathrm dz)/(\mathrm dt)+4z=e^(2t)\sin e^t`

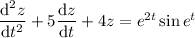
Of coursesin, the characteristic equation will be
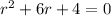
`r^2+6r+4=0`, which leads to solutions
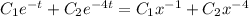
`C_1e^(-t)+C_2e^(-4t)=C_1x^(-1)+C_2x^(-4)`, as before.

Now that we have two linearly independent solutions, we can easily find more via variation of parameters. If
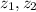
`z_1,z_2` are the solutions to the characteristic equation of the ODE in terms of
`z`, then we can find another of the form
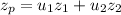
`z_p=u_1z_1+u_2z_2` where


`u_1=-\displaystyle\int(z_2e^(2t)\sin e^t)/(W(z_1,z_2))\,\mathrm dt`

`u_2=\displaystyle\int(z_1e^(2t)\sin e^t)/(W(z_1,z_2))\,\mathrm dt`

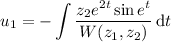
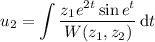
where
`W(z_1,z_2)` is the Wronskian of the two characteristic solutions. We have


`u_1=-\displaystyle\int(e^(-2t)\sin e^t)/(-3e^(-5t))\,\mathrm dt`

`u_1=\frac23(1-2e^(2t))\cos e^t+\frac23e^t\sin e^t`


`u_2=\displaystyle\int(e^t\sin e^t)/(-3e^(-5t))\,\mathrm dt`

`u_2=\frac13(120-20e^(2t)+e^(4t))e^t\cos e^t-\frac13(120-60e^(2t)+5e^(4t))\sin e^t`


`\implies z_p=u_1z_1+u_2z_2`

`\implies z_p=(40e^(-4t)-6)e^(-t)\cos e^t-(1-20e^(-2t)+40e^(-4t))\sin e^t`

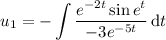
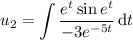
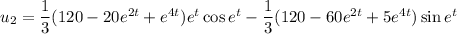
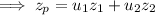
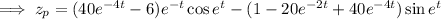
and recalling that
`t=\ln x\iff e^t=x`, we have


`\implies y_p=\left((40)/(x^3)-\frac6x\right)\cos x-\left(1-(20)/(x^2)+(40)/(x^4)\right)\sin x`