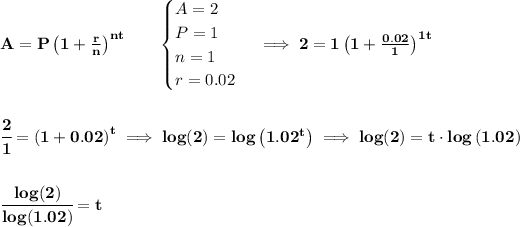Question

The balance A in a compound interest account with Principal(P), interest rate(r), conversion rate(m) and time(t) is given by: A=P(1+r/m)^mt

Suppose P= $1,000,000, r=2%/yr, m=2/yr
1) Find the balance A when t= 3 years.
2) Find the time t in case A= 2P. Express t in simplified exact form using log notation, then estimate t to the nearest year. You may use log2= 0.3010 and log1.01= 0.00432

Answer 1

1)

`\bf \qquad \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\to &\$1000000\\ r=rate\to 2\%\to (2)/(100)\to &0.02\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{is per year, thus once} \end{array}\to &1\\ t=years\to &3 \end{cases} \\\\\\ A=1000000\left(1+(0.02)/(1)\right)^(1\cdot 3)`

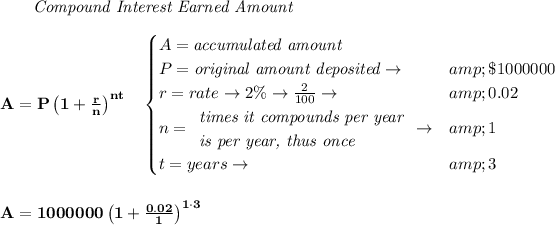
2)

now time "t" when A = 2P, if A = 2P, that means A is twice as much as P
or in short, the accumulated amount, is double the Principal, or that simply means, the time when the investment doubled

now, when that happens, hmm neverminding 1,000,000, let's just take $1 only, when that happens that $1 deposited, became $2 with interests

and for the sake of time, is the same as when 1,000,000 became 2,000,000

so, now, to get "t", we'll use the "bare" log, which when the base is skipped, simply means log base10, now, any base will do, we could have used ln() or natural logarithm, or logarithm base"e", just pointing that out


`\bf A=P\left(1+(r)/(n)\right)^(nt)\qquad \begin{cases} A=2\\ P=1\\ n=1\\ r=0.02 \end{cases}\implies 2=1\left(1+(0.02)/(1)\right)^(1t) \\\\\\ \cfrac{2}{1}=\left(1+0.02\right)^(t)\implies log(2)=log\left( 1.02^t \right) \implies log(2)=t\cdot log\left( 1.02 \right) \\\\\\ \cfrac{log(2)}{log(1.02)}=t`