Answer with explanation:
We will use angle bisector theorem to solve this problem.
Angle bisector theorem states that, the ratio of Adjacent sides containing the angle which is bisected is equal to the ratio of the segments where the angle bisector cuts the third side.
From the given Triangle
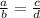
From the given information about the triangle, which is
An angle bisector of a triangle divides the opposite side of the triangle into segments of 5 cm and 3 cm long. A second side of the triangle is 7.6 cm long.
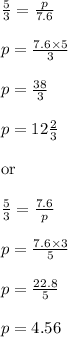
So,third Side of the triangle =4.56 cm ----Shortest possible length
Or, third Side of the triangle =
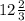 cm ----Largest possible length
cm ----Largest possible length