Question

Line m passes through the points (4, 1) and (7, 3) while line n passes through the points (-3, 5) and (-9, 1). Which statement accurately describes the relationship between the two lines?

A. Lines m and n have opposite reciprocal slopes so they are perpendicular.
B. Lines m and n have the same slope so they are perpendicular.
C. Lines m and n have the same slope so they are parallel.
D. Lines m and n have opposite reciprocal slopes so they are parallel.

Answer 1

The correct answer is C. Lines m and n have the same slope so they are parallel. The slope = 2/3

Answer 2

Answer: C. Lines m and n have the same slope so they are parallel.

Explanation:

We know that the the slope(m) of a line passing through points (a,b) and (c,d) is
`p=(d-b)/(c-a)`

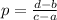
Thus, the slope of line m passes through the points (4, 1) and (7, 3) will be

`m_1=(3-1)/(7-4)=(2)/(3)`

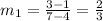
The slope of line n passes through the points (-3, 5) and (-9, 1) will be

`m_2=(1-5)/(-9-(-3))=(-4)/(-6)=(2)/(3)\\\Rightarrow\ m_2=(2)/(3)=m_1`

Therefore, Lines m and n have the same slope and if slopes of two lines are same then they are parallel.

Hence, Lines m and n have the same slope so they are parallel.