Question

The function f(t) = 30 sin (pi over 3t) −15 models the temperature of a periodic chemical reaction where t represents time in hours. What are the maximum and minimum temperatures of the reaction, and how long does the entire cycle take

Answer 1

f(t)=30 sin(pi/3 t)-15
when sin(pi/3 t) = 1, f(t) = 15 => max.
when sin(pi/3 t) = -1 f(t) = -45 .+ min.
period = 2π / (π/3) = 6 hrs.

Answer 2

The maximum temperatures of the reaction is 15 degree.

The minimum temperatures of the reaction is -45 degree.

The entire cycle take 6 hours.

Explanation:

Given : The function
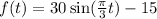`f(t) = 30 \sin ((\pi)/(3)t) -15` models the temperature of a periodic chemical reaction where t represents time in hours.

To find : What are the maximum and minimum temperatures of the reaction, and how long does the entire cycle take?

Solution :

We know that, sin function lies between -1 to 1.

So, The maximum and minimum points of sin x is 1 and -1 respectively.

Now, For maximum point

Substitute
`\sin ((\pi)/(3)t)=1`

`f(t) = 30(1) -15`

`f(t) = 15`

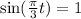
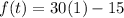
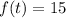
Now, For minimum point

Substitute
`\sin ((\pi)/(3)t)=-1`

`f(t) = 30(-1) -15`

`f(t) = -45`

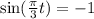
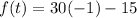
The maximum temperatures of the reaction is 15 degree.

The minimum temperatures of the reaction is -45 degree.

General form of sin function is
`y=A sin(Bx)+C`

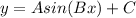
Where,

`B=\frac{2\pi}{\text{Period}}`

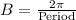
Comparing with given function,
`B=(\pi)/(3)`

`(\pi)/(3)=\frac{2\pi}{\text{Period}}`

`\text{Period}=(2\pi* 3)/(\pi)`

`\text{Period}=6`

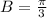
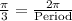
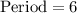
Therefore, The entire cycle take 6 hours.