Split up the interval [2, 5] into

equally spaced subintervals, then consider the value of

at the right endpoint of each subinterval.
The length of the interval is

, so the length of each subinterval would be

. This means the first rectangle's height would be taken to be
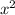
when
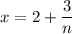
, so that the height is
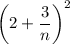
, and its base would have length
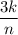
. So the area under
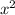
over the first subinterval is

.
Continuing in this fashion, the area under
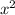
over the
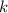
th subinterval is approximated by
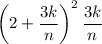
, and so the Riemann approximation to the definite integral is

and its value is given exactly by taking
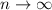
. So the answer is D (and the value of the integral is exactly 39).