Answer:
As we know that all conductors are equipotential so we can say that all points lie on the surface of conductors will be at same potential.
So here we can say that
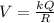
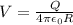
now we will multiply numerator and denominator by radius R
so here we will have
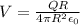
now we know that
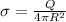
so we have
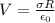
since potential is constant so here charge density and radius product will remain constant always
so here on spherical conductor the charge density will remain same at all points