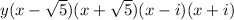Question

What is the completely factored form of x4y – 4x2y – 5y

Answer 1

y(x^2 - 5)(x^2 + 1)
I hope this helps!

Answer 2

Answer: The completely factored form is :

`y(x-√(5))(x+√(5))(x-i)(x+i)`

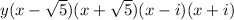
Explanation:

Since we have given that

`x^4y-4x^2y-5y`

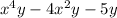
We just need to simplify the above expression:

1) Take the common factor 'y' from the expression:

`x^4y-4x^2y-5y\\\\=y(x^4-4x^2-5)`

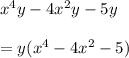
2) Split the middle term :

`y(x^4-4x^2-5)\\\\=y(x^4-5x^2+1x^2-5)\\\\=y(x^2(x^2-5)+1(x^2-5))\\\\=y(x^2-5)(x^2+1)\\\\`

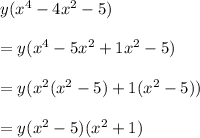
3) Completely factored form:

`y(x^2-5)(x^2+1)\\\\y(x-√(5))(x+√(5))(x-i)(x+i){\text{\{using }a^2-b^2=(a-b)(a+b)\}`

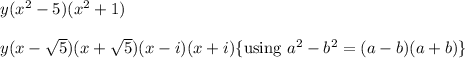
Hence, the completely factored form is :

`y(x-√(5))(x+√(5))(x-i)(x+i)`