Question

Please show your work to find the mean and standard deviation of the data. Round to the nearest tenth. 20, 16, 18, 14, 9, 20, 16

Answer 1

the mean is add all of them which is 113 then divide by 7 which is 16.14
the standard deviation is 3.85

Answer 2

Mean of given data is 16.15 and standard deviation is 3.56

Step-by-step explanation:

We have been given a data

`20,16,18,14,9,20,16`

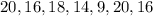
We need to find the mean and standard deviation:

mean=
`\frac{\text{sum of observations}}{\text{number of observations }}`

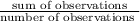
Here sum of observations are 20+16+18+14+9+20+16=113

Number of observations are 7

Substituting the values in the formula for mean we will get

`mean=(113)/(7 )=16.1428=16.15`

Formula for standard deviation is

`\sigma=\sqrt{\frac{\sum(x-\bar{x})^2}{n}}`

`\text{where, mean is }\bar{x}`

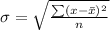
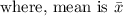
x are the values given for the data

n is 7 the number of observations

On substituting the values in the given formula we will get

`\sigma=\sqrt((20-16.15)^2+(16-16.15)^2+(18-16.15)^2+(14-16.15)^2+(9-16.15)^2+(20-16.15)^2+(16-16.15)^2)/(7)`

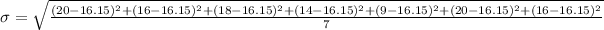
After simplification we will get

`\sigma=\sqrt((3.85)^2+(-0.15)^2+(1.85)^2+(-2.15)^2+(-7.15)^2+(3.85)^2+(-0.15)^2)/(7)`

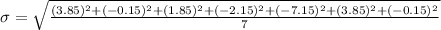
After further simplification we will get

`\sigma=\sqrt((14.8225)+(.0225)+(3.4225)+(4.6225)+(51.1225)+(14.8225)+(.0225))/(7)`

`\Rightarrow \sigma=\sqrt(88.8575)/(7)`

`\Rightarrow \sigma=√(12.6939)=3.56`

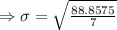
Therefore mean of given data is 16.15 and standard deviation is 3.56