Question

Instructions:Select the correct answer.

Which sequence is not equivalent to the others?
a reflection across the y-axis, followed by a reflection across the x-axis, and then a 90° clockwise rotation about the origin
a 90° clockwise rotation about the origin and then a 180° rotation about the origin
a reflection across the x-axis, followed by a 90° counterclockwise rotation about the origin, and then a reflection across the x-axis
a 90° counterclockwise rotation about the origin
NextReset

Answer 1

the second one is correct

Answer 2

The correct option is 3.

Explanation:

Option 1,

A reflection across the y-axis,

`P(x,y)\rightarrow P_1(-x,y)`

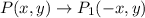
then reflection across the x-axis

`(x,y)\rightarrow (x,-y)`

`P_1(-x,y)\rightarrow P_2(-x,-y)`

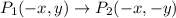
and then a 90° clockwise rotation about the origin.

`(x,y)\rightarrow (y,-x)`

`P_2(-x,-y)\rightarrow P_3(-y,x)`

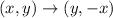
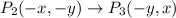
So the image of P(x,y) is P'(-y,x).

Option 2,

A 90° clockwise rotation about the origin

`P(x,y)\rightarrow P_1(y,-x)`

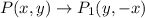
and then a 180° rotation about the origin.

`(x,y)\rightarrow (-x,-y)`

`P_1(y,-x)\rightarrow P_2(-y,x)`

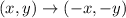
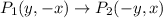
So the image of P(x,y) is P'(-y,x).

Option 3,

A reflection across the x-axis,

`P(x,y)\rightarrow P_1(x,-y)`

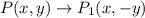
Followed by a 90° counterclockwise rotation about the origin.

`(x,y)\rightarrow (-y,x)`

`P_1(x,-y)\rightarrow P_2(y,x)`

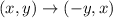
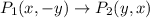
and then a reflection across the x-axis.

`(x,y)\rightarrow (x,-y)`

`P_2(y,x)\rightarrow P_3(y,-x)`

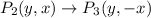
So the image of P(x,y) is P'(y,-x).

Option 4,

A 90° counterclockwise rotation about the origin

`P(x,y)\rightarrow P_1(-y,x)`

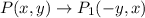
So the image of P(x,y) is P'(-y,x).

The third sequence is not equivalent to the others. Therefore the correct option is 3.