Question

Which condition is necessary for total internal reflection?

Answer 1

Total internal reflection occurs when the incident angle in the first medium is greater than the critical angle. It results in all the light being reflected back into the first medium.

Step-by-step explanation:

Total internal reflection is a phenomenon that occurs at the boundary between two media. It happens when the incident angle in the first medium is greater than the critical angle. The critical angle is the incident angle that produces an angle of refraction of 90°. When total internal reflection occurs, all the light is reflected back into the first medium, and none of it is transmitted into the second medium.

Answer 2

The index of refraction of the first medium must be higher than the index of refraction of the second medium

Step-by-step explanation:

Snell's law describes the behaviour of light at the boundary between two mediums:

`n_1 sin \theta_1 = n_2 sin \theta_2`

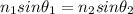
where

n1 and n2 are the index of refraction of the two mediums

`\theta_1, \theta_2` are the angle between the direction of the light ray and the normal to the interface

We can rewrite the condition as:

`sin \theta_2 = (n_1)/(n_2) sin \theta_1`

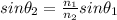
Let's assume now that the light is travelling in the first medium with a very large angle with respect to the normal to the surface, i.e.
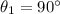`\theta_1 = 90^(\circ)`, so that
`sin \theta_1=1`. In this case, we have

`sin \theta_2 = (n_1)/(n_2)`

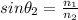
We notice that if
`n_1 > n_2`, the ratio on the right is larger than 1, and so the term
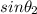`sin \theta_2` should be also larger than 1: but this is not possible of course, since the sine function is always less than 1. Therefore, in this case total internal reflection occurs, because no refracted ray is produced.