Question

Which expression represents (−21−−−−√5)6 in rational exponent form? (−21)6/5 −215/6 (65)−21 (56)−21

Answer 1

`(-21)^(6)/(5)`

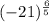
Explanation:

Which expression represents [⁵√(−21)]⁶ in rational exponent form?

Solution:

Rational numbers are numbers which can be expressed as fractions in the form a / b, where a, b are integers and b is not equal to zero.

A rational exponent is an exponent that is a fraction. For example √2 =
`2^(1)/(2)`.

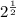When expressing a number in rational exponent form, the numerator of the fractional exponent refers to a normal power, but the denominator refers to the root.

`[\sqrt[5]{(-21)}]^6 = (-21)^(6)/(5)`