Answer:
Explanation:
Alright, lets get started.
The given velocity is 150.
Please refer the diagram I have attached.
The horizontal component is =
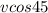
The horizontal component is =
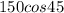
The horizontal component is = 106.06 : Answer
The vertical component is =
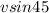
The vertical component is =

The vertical component is = 106.06 : Answer