Answer : The concentration of
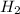 at equilibrium is 0.012 M
at equilibrium is 0.012 M
Solution :
First we have to calculate the concentration of
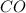 and
and
 .
.
Concentration of
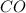 =
=
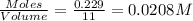
Concentration of
 =
=
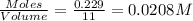
The given equilibrium reaction is,
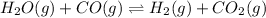
Initially conc. 0.0208 0.0208 0 0
At equilibrium. (0.0208-x) (0.0208-x) x x
The expression of
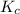 will be,
will be,
![K_c=([H_2][CO_2])/([H_2O][CO])](https://img.qammunity.org/2018/formulas/chemistry/high-school/aa34yvzoeujg2lurtd7n8z9be3uwh65i51.png)
For given reaction the value of
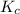 will be,
will be,
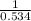 (for reverse reaction).
(for reverse reaction).
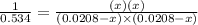
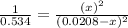
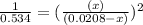
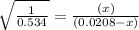
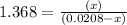
By solving the term x, we get
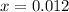
Thus, the concentration of
 at equilibrium = x = 0.012 M
at equilibrium = x = 0.012 M