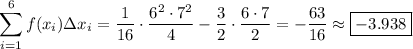Question

Evaluate the Riemann sum for (x) = x3 − 6x, for 0 ≤ x ≤ 3 with six subintervals, taking the sample points, xi, to be the right endpoint of each interval. Give three decimal places in your answer.

Answer 1

Split up the interval [0, 3] into 6 subintervals. Each will have length

`\Delta x_i = \frac{3-0}6 = \frac12`

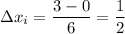
So the partition will be

[0, 1/2], [1/2, 1], [1, 3/2], [3/2, 2], [2, 5/2], [5/2, 6]

The right endpoints form an arithmetic sequence given by

`x_i = \frac i2`

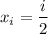
where 1 ≤ i ≤ 6.

Then the Riemann sum is

`\displaystyle \sum_(i=1)^6 f(x_i) \Delta x_i = \frac12 \sum_(i=1)^6 \left(\left(\frac i2\right)^3 - 6\left(\frac i2\right)\right)`

`\displaystyle \sum_(i=1)^6 f(x_i) \Delta x_i = \frac12 \sum_(i=1)^6 \left(\frac{i^3}8 - 3i\right)`

`\displaystyle \sum_(i=1)^6 f(x_i) \Delta x_i = \frac1{16} \sum_(i=1)^6 i^3 - \frac32 \sum_(i=1)^6 i`

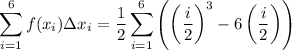
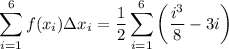
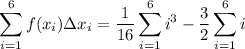
Recall the formulas for sums of powers:

`\displaystyle \sum_(i=1)^n i = \frac{n(n+1)}2`

`\displaystyle \sum_(i=1)^n i^3 = \frac{n^2(n+1)^2}4`

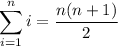
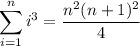
It follows that

`\displaystyle \sum_(i=1)^6 f(x_i) \Delta x_i = \frac1{16} \cdot \frac{6^2\cdot7^2}4 - \frac32 \cdot \frac{6\cdot7}2 = -(63)/(16) \approx \boxed{-3.938}`