Question

A carton of milk has spilled on a tile floor. The milk flow can be expressed with the function m(t) = 9t, where t represents time in minutes and m represents how far the milk is spreading. The flowing milk is creating a circular pattern on the tile. The area of the pattern can be expressed as A(m) = πm2. Part A: Find the area of the circle of spilled milk as a function of time, or A[m(t)]. Show your work. (6 points) Part B: How large is the area of spilled milk after 2 minutes? You may use 3.14 to approximate π in this problem.

Answer 1

Part A: A(m(t)) = π(81t²); Part B: 1017.36

Step by step explanation:

Part A:

To find A(m(t)), we substitute our value for m(t), 9t, in place of m:

A(m(t)) = πm² = π(9t)² = π(81t²)

A(m(t)) = π(81t²)

Part B:

Substitute 2 in for t:

A(m(2)) = π(81(2²)) = π(81(4)) = 3.14(324) = 1017.36

Answer 2

As per the statement:

The milk flow can be expressed with the function:

`m(t) = 9t` where, t represents time in minutes and m represents how far the milk is spreading.

The flowing milk is creating a circular pattern on the tile.

The area of the pattern can be expressed as:

`A(m) = \pi m^2`

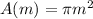
Part A.

Find the area of the circle of spilled milk as a function of time, or A[m(t)].

Substitute m(t) = 9t in A[m] we have;

`A[m(t)] = \pi \cdot (m(t))^2 = \pi \cdot (9t)^2 = 81t^2 \pi` .....[1]

⇒
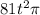`81t^2 \pi` is the area of the circle of spilled milk as a function of time, or A[m(t)].

Part B.

How large is the area of spilled milk after 2 minutes

Substitute t = 2 minutes and Use
`\pi = 3.14` in [1] we have;

`A[m(2)] = 81 \cdot (2)^2 \cdot 3.14 = 81 \cdot 4 \cdot 3.14 = 1,017.36`

Therefore, 1017.36 square unit is the area of spilled milk after 2 minutes