Question

Not good with these types of questions anyone good at this help please?!

Answer 1

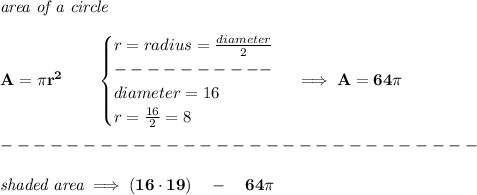
now, notice the picture below

is really just one rectangle and a circle, well, half a circle or a semi-circle

so.... if you get the area of the whole rectangle, 16*19
and subtract, the area of half the circle, you end up with the shaded area

since, what you'd be leftover is, the rectangle, with a semi-circular hole, that was subtracted


`\bf \textit{area of a circle}\\\\ A=\pi r^2\qquad \begin{cases} r=radius=(diameter)/(2)\\ ----------\\ diameter=16\\ r=(16)/(2)=8 \end{cases}\implies A=64\pi \\\\ -----------------------------\\\\ \textit{shaded area}\implies (16\cdot 19)\quad -\quad 64\pi`


now... let's say, you get an amount of hmmm [?]
ok, how much is that in percentage? well, 16*19 is 304

so, if we take 304 as the 100%, how much is [?] in percentage?


`\bf \begin{array}{ccllll} amount&\%\\ \textendash\textendash\textendash\textendash\textendash\textendash&\textendash\textendash\textendash\textendash\textendash\textendash\\ 304&100\\ \boxed{?}&x \end{array}\implies \cfrac{304}{\boxed{?}}=\cfrac{100}{x}`

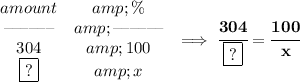
solve for "x"