Question

In sunlight, a vertical stick has a height of 5 ft and casts a shadow 3 ft long at the same time that a nearby tree casts a shadow 15 ft long. How tall is the tree?

Answer 1

The tree is 25 ft tall.

Explanation:

Since, at the same time the ratio of actual height and shadow is constant for every object.

Thus, we can write,

At the same time,

`\frac{\text{Height of tree}}{\text{Length of its shadow}}=\frac{\text{Height of vertical stick}}{\text{length of its shadow}}`

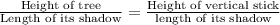
Given,

The vertical stick has a height of 5 ft and casts a shadow 3 ft long at the same time that a nearby tree casts a shadow 15 ft long,

Let h be the height of the tree,

`\implies (h)/(15)=(5)/(3)`

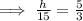
By cross multiplication,

`3h=75`

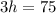
Dividing both sides by 3,

`h=25`

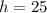
Hence, the tree is 25 ft tall.

Answer 2

The tree is 25 feet tall. Given the height of the stick and the shadow it cast, the angle formed by the sun and the stick's height can be obtained by taking the Inverse Tangent of 3/5. This is equal to 30.93. This angle is equal to the angle formed by the sun and the tree's height. Using the tangent formula, Tan (30.93)=tree's shadow (15 ft)/ height of the tree, giving the answer 25 feet.