Question

Maureen is taking an antibiotic. The table below shows the amount of antibiotic f(t), in mg, that was present in her body after time t: t (hours) 1 2 3 4 5 f(t) (mg) 150 90 54 32.4 19.4 Ken was administered 200 mg of the same antibiotic. The amount of antibiotic f(t) in his body after time t is shown by the equation below: f(t) = 200(0.976)t Which statement best describes the rate at which Maureen's and Ken's bodies eliminated the antibiotic? Maureen's body eliminated the antibiotic faster than Ken's body. Maureen's body eliminated the antibiotic at the same rate as Ken's body. Maureen's body eliminated the antibiotic at half of the rate at which Ken's body eliminated the antibiotic. Maureen's body eliminated the antibiotic at one-fourth of the rate at which Ken's body eliminated the antibiotic.

Answer 1

Maureen's body eliminated the antibiotic faster than Ken's body.

Explanation:

To find the rate at which Maureen's body uses the antibiotic, we find the percent of change. To do this, we use the formula

`\text{percent of change}=\frac{\text{amount of change}}{\text{original amount}}`

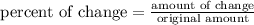
Between hour 1 and hour 2, the amount of change was 150-90 = 60. The "original amount" between these two is 150; this gives us

60/150 = 0.4

Between hour 2 and hour 3, the amount of change was 90-54 = 36. The "original amount" was 90; this give us

36/90 = 0.4

Between hour 3 and hour 4, the amount of change was 54-32.4 = 21.6. The "original amount" was 54; this gives us

21.6/54 = 0.4

Between hour 4 and hour 5, the amount of change was 32.4-19.4 = 13. The "original amount" was 32.4; this gives us

13/32.4 = 0.40

Her body had 100%-40% = 60% of the antibiotic remaining after each hour.

We can analyze Ken's function to see how much his body used. His function is of the form

f(x) = a*bˣ,

where a represents the original amount, b represents 1 + the rate of change, and x represents the amount of time.

In place of a in Ken's function, we see 200; this is the amount he was originally given.

In place of b, we see 0.976; this means we have subtracted something from 1:

1-0.976 = 0.024

Ken uses 0.024 = 2.4% of the antibiotic per hour.

Maureen uses it up more quickly.

Answer 2

Maureen's body eliminated the bacteria faster then Ken's as if you multiply 150 times 0.976 you get a number larger then 90 so Ken would have eliminated 150 mg of antibiotics slower then Maureen.