Question

create a perfect square trinomial that can be factored using special patterns. Factor the trinomial and show all work for full credit.

Answer 1

Answer:
`4x^2+12x+9`

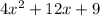
Explanation:

A perfect square trinomial is written as
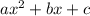`ax^2+bx+c`, where

first term
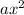`ax^2` = square of first term of binomial

second term=
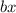`bx`=twice the product of both terms of binomial.

and third term 'c'=square of last term of binomial

Thus to create a perfect square trinomial put 'a' and 'c' a square number

Let a=4 and c=9

The required trinomial will be

`4x^2+12x+9`

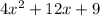
`=(2x)^2+2(2x)(3)+3^2\\=(2x+3)^2.......\text{[using pattern}(a+b)^2=a^2+2ab+b^2]\\=(2x+3)(2x+3)`

Answer 2

trinomial is 3 terms
ax^2+bx+c
4 is a perfect square since 2*2
essentially, you need (x+a)^2
(x+1)^2=(x+1)(x+1)=x^2+2x+1
as far as "special patterns" this may imply that you need to find a perfect square trinomial that requires a different factoring process, I'm not sure what that means