answer : A , C , D
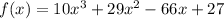
WE plug in each root in f(x) and check whether we get value =0
When f(a) =0 then 'a' is the actual root
Lets start with -9/2, plug in -9/2 for x
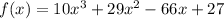
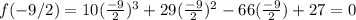
Hence -9/2 is one of the actual root
now plug in -9/10 for x
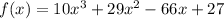
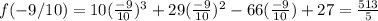
Hence -9/10 is not an actual root
now plug in 3/5 for x
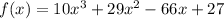
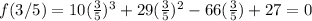
So 3/5 is one of the actual root
Now plug in 1 for x
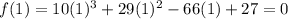
So 1 is one of the actual root
Now plug in 3 for x
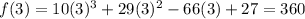
So 3 is not the actual root
Answer is -9/2 , 3/5 and 1