Answer:
A= (-6, 2)
Explanation:
Let (
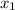
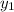 ) be the coordinates of A , let (
) be the coordinates of A , let (
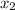 ,
,
 ) be the coordinate of B
) be the coordinate of B
and let (
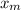 ,
,
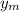 ) be the midpoints of segment AB
) be the midpoints of segment AB
To find the coordinates of A, we simply use the formula for calculating mid-points of segment
(
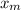 ,
,
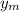 ) =
) =
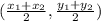
From the formula above;
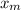 =
=
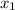 +
+
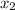 / 2 ---------------(1)
/ 2 ---------------(1)
Similarly
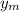 =
=
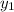 +
+
 / 2 --------(2)
/ 2 --------(2)
From the question given;
(
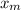 ,
,
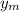 ) = (-3, 2) which implies:
) = (-3, 2) which implies:
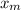 = -3 and
= -3 and
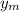 = 2
= 2
similarly (
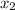 ,
,
 ) = (0,2) this implies that
) = (0,2) this implies that
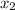 = 0 and
= 0 and
 =2
=2
From equation (1)
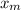 =
=
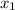 +
+
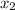 / 2
/ 2
we substitute
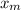 = -3 and
= -3 and
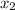 = 0 into equation (1) to get
= 0 into equation (1) to get
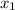
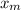 =
=
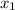 +
+
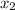 / 2
/ 2
-3 =
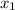 + 0 / 2
+ 0 / 2
cross multiply
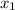 + 0 = -3 × 2
+ 0 = -3 × 2
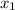 = -6
= -6
Also;
We substitute;
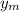 = 2 and
= 2 and
 =2 into equation (2)
=2 into equation (2)
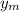 =
=
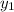 +
+
 / 2 --------(2)
/ 2 --------(2)
2 =
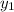 + 2 / 2
+ 2 / 2
cross multiply
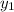 + 2 = 2 × 2
+ 2 = 2 × 2
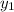 + 2 = 4
+ 2 = 4
subtract 2 from both-side of the equation
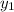 + 2 -2 = 4 -2
+ 2 -2 = 4 -2
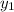 = 2
= 2
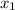 = -6 and
= -6 and
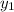 = 2
= 2
Therefore; Coordinate of A (
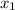
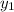 ) = (-6, 2)
) = (-6, 2)