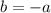Answer:
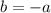
Explanation:
Direct variation says that:
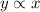 then,
then,
equation is in the form of:
 where, k is the constant of variation.
where, k is the constant of variation.
As per the statement:
A number b varies directly with the number a.
by definition we have;
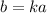
Substitute b = 2 and a = -2 we have;

Divide both sides by -2 we have;
-1 = k
or
k = -1
Then, equation we get;
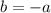
Therefore, equation represents this direct variation between a and b is: