Question

A satellite originally moves in a circular orbit of radius R around the Earth. Suppose it is moved into a circular orbit of radius 4R. What happens to the satellite's speed?

Answer 1

satellite originally moves in a circular orbit of radius R around the Earth. Suppose it is moved into a circular orbit of radius 4R.

(i) What does the force exerted on the satellite then become?

eight times largerfour times larger one-half as largeone-eighth as largeone-sixteenth as large(ii) What happens to the satellite's speed?eight times largerfour times larger one-half as largeone-eighth as largeone-sixteenth as large(iii) What happens to its period?eight times largerfour times larger one-half as largeone-eighth as largeone-sixteenth as large

Answer 2

The speed of satellite moving into circular orbit of radius 4R will become half of the speed of satellite moving into circular orbit of radius R.

Step-by-step explanation:

Speed of satellite revolving around the central body in a circular path:

`v=\sqrt{(G* M)/(R)}`

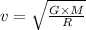
Where :

G = gravitational constant =
`6.673 * 10^(-11) Nm^2/kg^2]`

M = Mass of body around which satellite is orbiting

R = radius of the orbit from the satellite

A satellite originally moves in a circular orbit of radius R around the Earth.The velocity of satellite will be ;

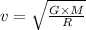`v=\sqrt{(G* M)/(R)}`..[1]

If the same satellite moves in a circular orbit of radius $R around the Earth.The speed of satellite will be :

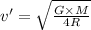`v'=\sqrt{(G* M)/(4R)}`..[2]

Dividing [1] and [2]:

`(v)/(v')=\frac{\sqrt{(G* M)/(R)}}{\sqrt{(G* M)/(4R)}}`

`(v)/(v')=2`

`v'=(1)/(2)v`

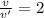
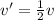
The speed of satellite moving into circular orbit of radius 4R will become half of the speed of satellite moving into circular orbit of radius R.