Answer:
1. D
2.B
3.B
4.B
5. B
6.D
Explanation:
QUESTION 1
We want to simplify
 .
.
Let us change the middle bar to a normal division sign to obtain,
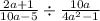 .
.
We now multiply, the first fraction by the reciprocal of the second fraction to get,
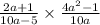 .
.
We now factor to obtain,
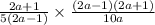 .
.
We cancel out common factors to get,
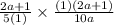 .
.
We now multiply out to get,
 .
.
Ans:D
QUESTION 2
The given expression is

We change the middle bar to a normal division sign to get,
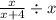
We now multiply by the reciprocal of the second fraction to obtain,
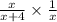
Ans:B
QUESTION 3
We want to simplify the quotient,
 .
.
We change the middle to a normal division sign to obtain,
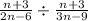 .
.
We now multiply the first fraction by the reciprocal of the second fraction to get,
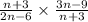 .
.
We factor to get,
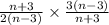 .
.
We cancel out common factors to obtain,
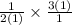 .
.
We simplify to get,
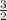 .
.
Ans:B
QUESTION 4
We want to find the product
 .
.
This multiplication is very simple to do. We just have to cancel out common factors to get,
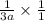 .
.
We now multiply out to get,
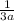
Ans:B
QUESTION 5.
We want to find the product
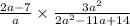 .
.
We factor the denominator of the second fraction to obtain,
 .
.
We now cancel out common factors to obtain,
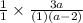 .
.
We multiply out to get,
 .
.
Ans:B
QUESTION 6
We want to find the quotient
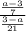 .
.
We need to change the middle bar to a normal division sign to get,
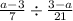
We multiply by the reciprocal of the second function to get,

We factor the negative 1 from the denominator of the second fraction to get,
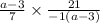
We now cancel common factors to get,

This simplifies to,
 .
.
Ans: D
Two questions repeated