Question

Heat is added to each block at the same constant rate until it reaches a temperature of 500 k. which of the following statements is true? the specific heat capacity of aluminum is about twice that of iron. consider two blocks of equal mass, one made of aluminum and the other one made of iron, initially in thermal equilibrium.

Answer 1

I think the correct answer would be that the specific heat capacity of aluminum is about twice that of iron. Heat is added to the blocks at a rate that is constant. The block that had reached the final temperature in the least time is the one that needs the least amount of heat which would be iron.

Answer 2

The given question is incomplete. Complete question is as follows.

The specific heat capacity of aluminum is about twice that of iron. Consider two blocks of equal mass, one made of aluminum and the other one made of iron, initially in thermal equilibrium.

Heat is added to each block at the same constant rate until it reaches a temperature of 500 K. Which of the following statements is true?

The iron takes less time than the aluminum to reach the final temperature.

The aluminum takes less time than the iron to reach the final temperature.

The two blocks take the same amount of time to reach the final temperature.

When the two materials have reached thermal equilibrium, the block of aluminum is cut in half and equal quantities of heat are added to the iron block and to each portion of the aluminum block. Which of the following statements is true?

The three blocks are no longer in thermal equilibrium; the iron block is warmer.

The three blocks are no longer in thermal equilibrium; both the aluminum blocks are warmer.

The blocks remain in thermal equilibrium.

Step-by-step explanation:

According to the question, rate of heat supplied to the iron is equal to the rate of heat supplied to the aluminium block.

`(Q_(I))/(t_(I)) = (Q_(Al))/(t_(Al))`

`(mC_(I) \Delta T)/(t_(I)) = (mC_(Al) \Delta T)/(t_(Al))`

`(mC_(I) \Delta T)/(t_(I)) = (m(2C_(I)) \Delta T)/(t_(Al))`

`t_(Al) = 2t_(I)`

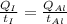
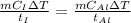
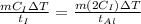
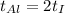
This means iron take less time to reach the final temperature as compared to aluminium.

But heat supplied to both the blocks is same.

`Q_(I) = Q_(Al)`

`mC_(I) \Delta T_(I) = ((m)/(2))C_(Al) \Delta T_(Al)`

`mC_(I) \Delta T_(I) = ((m)/(2))2C_(I) \Delta T_(Al)`

`\Delta T_(I) = \Delta T_(Al)`

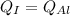
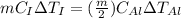
As the change in temperature is equal. So, both the blocks will remain in thermal equilibrium.