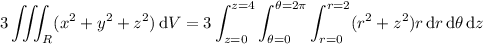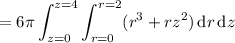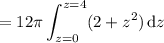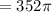Use the divergence theorem. Let
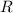
be the cylindrical region, then
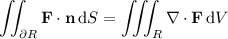
(where

denotes the unit normal vector to
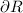
, but we don't need to worry about it now)
We have
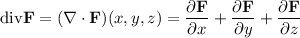
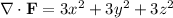
For the solid
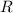
with boundary
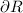
, we can set up the following volume integral in cylindrical coordinates for ease: