Answer:
Option (a), (d) and (e) are correct.
Explanation:
Given : expression

We have to select the equivalent fractions from the given options.
We will check each given option one by one,
a)
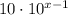
Apply property of exponents,
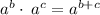
We have,
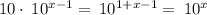
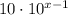 is equivalent to given expression
is equivalent to given expression

b)

Breaking 50 into factor as
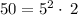
Thus,
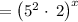
Apply exponent rule ,
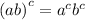
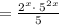
Apply exponent rule ,
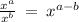
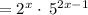
 is not equivalent to given expression
is not equivalent to given expression

c)
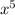
Clearly seen
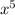 is not equivalent to given expression
is not equivalent to given expression

d)
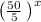
Divide 50 by 5 we have 10
So
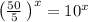
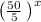 is equivalent to given expression
is equivalent to given expression

e)
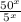
Breaking 50 into factor as
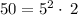
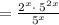
Apply exponent rule ,
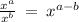

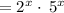
Apply exponent rule
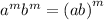
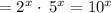
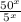 is equivalent to given expression
is equivalent to given expression

f)
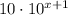
Apply property of exponents,
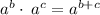
We have,
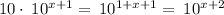
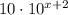 is not equivalent to given expression
is not equivalent to given expression

Thus, option (a), (d) and (e) are correct.