Answer:
Juanita is standing 31.17 ft far from the tree.
Explanation:
Angle of elevation measured by Juanita =
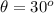
Height of the tree = 18 ft
Also, an image of that tree whose height is 18 ft and its top is making an angle of 30°.This means length of the image is equal to the distance at which Juanita is standing.
In fig ΔABC
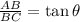
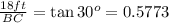 (tan 30° = 0.5773)
(tan 30° = 0.5773)
BC = 31.17 ft ≈ 31.2 ft
Juanita is standing 31.2 ft far from the tree.