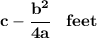Question

Suppose a punter kicks a football so that the upward component of its velocity is 80 feet per second. If the ball is 3 feet off the ground when it is kicked, then the height of the ball, in feet, t seconds after it is kicked is given by h(t) = 3 + 80t - 16t2.

a. Find the upward velocity v(t) of the football.
b. How fast is the ball travelling upward 1 second after it is kicked?
c. Find the time when the ball reaches its maximum height.
d. What is the maximum height of the ball?

Answer 1

so hmm check the picture below


`\bf \qquad \textit{initial velocity}\\\\ h = -16t^2+v_ot+h_o \qquad \text{in feet}\\ \\ v_o=\textit{initial velocity of the object}\\ h_o=\textit{initial height of the object}\\ h=\textit{height of the object at`

a)

well, clearly is 80 ft/s

b)

when t = 1? well 80(1)

c)

in the picture, x-axis is the time and y-axis is the height
so, it reaches its maximum at the vertex, after "x" seconds


`\bf \begin{array}{lcccll} h(t)=&-16t^2&+80t&+3\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array}\qquad \left(-\cfrac{{{ b}}}{2{{ a}}}\quad ,\quad {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\right)`

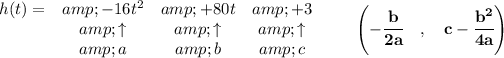
so it reached the vertex after
`\bf -\cfrac{{{ b}}}{2{{ a}}}\quad seconds`

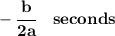
d)

the maximum height of the ball is
`\bf {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\quad feet`