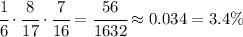Question

A bowl contains 3 red, 8 blue, and 7 black beads. Margaret randomly selects 3 beads one after the other without replacement. Find the probability of getting a red, blue, and black bead, in that order.

Answer 1

This experiment consists in three phases: let's analyse each phase and the correspondent probability.

At the beginning, we have
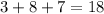`3+8+7 = 18` beads. 3 of them are red. So, we have a probability of
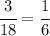`\cfrac{3}{18} = \cfrac{1}{6}` of selecting a red bead.

Suppose we do select a red bead with the first pick. Let's analyse the new scenario. Now we're left with
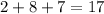`2+8+7 = 17` beads, and 8 of them are blue. So, we have a probability of
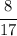`\cfrac{8}{17}` of selecting a blue bead.

And if we do, we arrive to the last scenario: we have
`2+7+7 = 16` beads, and 7 of them are black. So, we have a probability of
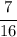`\cfrac{7}{16}` of selecting a black bead.

So, in order to getting a red, blue, and black bead, in that order, three events must happen one after the other, and we know their individual probability. The result is thus the product of these probabilities, namely

`\cfrac{1}{6}\cdot \cfrac{8}{17} \cdot \cfrac{7}{16} = \cfrac{56}{1632} \approx 0.034 = 3.4\%`