Question

(Solve the problem & round the final answer to four decimal places.)

Answer 1

Given: The logarithm below

`log_7√(3)`

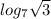
To Determine: The solution of the given

Solution

Using exponent rule below

`√(a)=a^{(1)/(2)}`

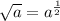
Applying the exponent rule above to the given logarithm

`\begin{gathered} log_7√(3) \\ √(3)=3^{(1)/(2)} \\ Therefore \\ log_7√(3)=log_73^{(1)/(2)} \end{gathered}`

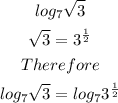
Using logarithm rule to the given

`\begin{gathered} log_ab^x=xlog_ab \\ Therefore \\ log_73^{(1)/(2)}=(1)/(2)log_73 \end{gathered}`

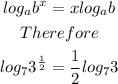
Let us apply change of base as shown below

`log_73=(log_e3)/(log_e7)`
`\begin{gathered} Log_e3=ln3=1.09861 \\ log_e7=ln7=1.94591 \\ log_73=(log_e3)/(log_e7)=(ln3)/(ln7)=(1.09861)/(1.94591)=0.56457 \end{gathered}`

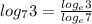
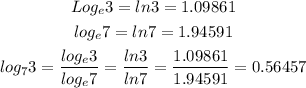
Therefore, we have

`log_7√(3)=(1)/(2)log_73=(1)/(2)*0.56457=0.28228\approx0.2823(4decimal-place)`

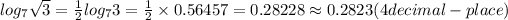
Hence, the final answer is approximately 0.2823