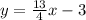The function is given to be:
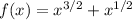
at (4, 10).
Step 1: Differentiate the function
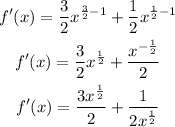
Step 2: Substitute for x = 4 into f'(x)
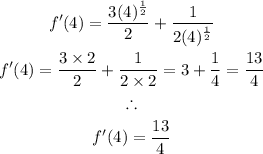
Step 3: Find a line with the slope 13/4 passing through (4, 10) using the point-slope form of the equation of a straight line given to be
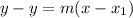
Therefore, we have:
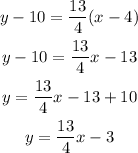
ANSWER
The equation of the tangent at the point is: