Question

What is the perimeter of rhombus wxyz?

A.square root 13 units
B.12 units
C.4 square root 13 units
D.20 units

Answer 1

For this case, the first thing we must do is define the formula of distance between points.

We have then:

`d = √((x2-x1)^2 + (y2-y1)^2)`

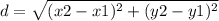
From here, we look for the distance between two points of rhombus.

`image`

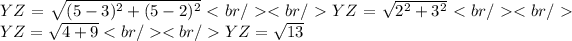
Then, since all sides have the same length, then the perimeter is given by:

`P = 4YZ`

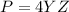
Substituting we have:

`P = 4√(13)`

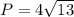
Answer:

The perimeter of the rhombus is:

`P = 4√(13)`

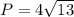
option 3

Answer 2

One of the properties of rhombus is its sides are congruent. Therefore, we will only need to find the length of one side using the distance formula. At line YZ, the distance is
`\sqrt{ (x_(2) -x_(1) )^(2) +(y_(2) -y_(1) )^(2)}`

D =
`\sqrt{ (5 -3 )^(2) +(5 -2) ^(2) }` = √13

To get the perimeter, multiply one side to 4. Hence, the perimeter is 4√13 (C)