Question

How many extraneous solutions does the equation below have?

(2m)/(2m+3)-(2m)/(2m-3)=1
0
1
2
3

Answer 1

The given equation with solution is

`(2 m)/(2 m+3)-(2 m)/(2 m-3)=1\\\\ 2m((1)/(2m+3)-(1)/(2 m-3))=1\\\\ 2 m*(2m-3-2m-3)/((2m+3)(2m-3))=1\\\\ -12 m=4m^2-9\\\\ 4m^2+12 m-9=0\\\\ m=(-12 \pm√((12)^2-4* 4 * (-9)))/(2* 4)\\\\ m=(-12\pm√(288))/(8)\\\\ m=(12)/(8)*(-1\pm√(2))\\\\ m=(3)/(2)*(-1\pm√(2))`

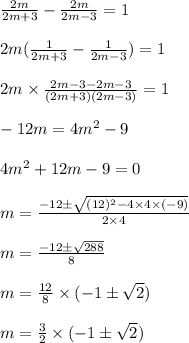
The formula used to find the roots is

`x=(-b\pm√(b^2-4ac))/(2a)`

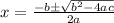
If it is a quadratic equation of type , a x²+bx+c=0

→→As, both the roots , which is ,
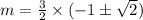`m=(3)/(2)*(-1\pm√(2))` satisfy the equation given.That is when you substitute the value of m in equation given , we get LHS=RHS.

So, there are no ,extraneous solution of the equation provided.

A solution set is said to be extraneous , if the roots obtained of the equation does not satisfy the equation provided.

Option (A) 0, is right choice.

Answer 2

0

Step-by-step explanation

(2m)/(2m+3)-(2m)/(2m-3)=1

Simplifying the left hand first

(2m)/(2m+3)-(2m)/(2m-3) = {2m(2m-3) - 2m(2m+3)}/(4m²-9)

(4m²-6m-4m²-6m)/(4m²-9)

= (-12m) / (4m²-9)

Now this equet to 1

(-12m) / (4m²-9) = 1

-12m = 4m²-9

4m²+ 12m -9 =0 ⇒⇒⇒ This is a quadratic equation that has 2 real solutions.

4m²+ 12m -9 =0

m² + 3m + (3/2)²= 9/4 + 9/4

(m + 3/2)² = 18/4

m = √18/2 - 3/2 or m = -√18/2 - 3/2

= 0.621 = -3.621

So we can say that the equation has NO extraneous solutions.

Answer = 0