Answer with explanation:
Number of Students in the Class =160
Out of which,
Number of honor Students = 40
Number of Athletes = 60
Number of Students who are neither athletes nor honor students=80
⇒ Total Number of students in the class - n (A ∪ B)= 80
⇒160 -80=n(A∪B)
⇒n (A ∪ B)=80
⇒n (A ∪ B)=n(A) + n(B) - n(A ∩ B)
⇒80= 40 +60 - n(A ∩ B)
⇒n (A ∩ B)= 100 -80
⇒n (A ∩ B)= 20
Two events A and B are Said to be Independent, if
⇒P (A ∩ B)=P (A) × P (B)
Probability of an event is defined as total favorable outcome divided by total possible outcome.
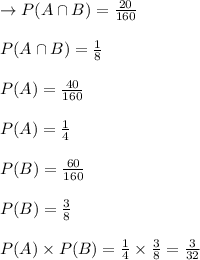
We see that,
⇒P (A ∩ B)≠P (A) × P (B)
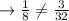
so,the events are not independent.