Answer:
22.4%
Explanation:
We have the events,
A = The driver got in an accident
B = The driver took the safety test
Now, it is required to find the conditional probability P(A|B).
Since,
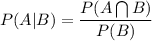
From the table, we have that,

Thus, we get,
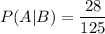
i.e. P(A|B) = 0.224
i.e. P(A|B) = 22.4%
Hence, the probability that the driver got in an accident even though the driver took the safety test is 22.4%