Question

Which statement best describes how to determine whether f(x) = 9 – 4x2 is an odd function? Determine whether 9 – 4(–x)2 is equivalent to 9 – 4x2. Determine whether 9 – 4(–x2) is equivalent to 9 + 4x2. Determine whether 9 – 4(–x)2 is equivalent to –(9 – 4x2). Determine whether 9 – 4(–x2) is equivalent to –(9 + 4x2).

Answer 1

The answer is C) Determine whether 9 – 4(–x)^2 is equivalent to –(9 – 4x^2)

Answer 2

We have a property for odd functions, which is given below. Let f(x) be an odd function then it must satisfy the below - mentioned property.

`f(-x)= -f(x)`

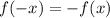
Now, we have been given the function
`f(x)=9-4x^2`

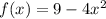
For this function to be odd, it must satisfy the above written property.

Replace x with -x, we get

`f(-x)=9-4(-x)^2`

And, we have to also find

`-f(x)=-(9-4x^2)`

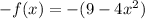
Hence, in order to the given function to be an odd function, we must determine whether 9-4(-x)^2 is equivalent to -(9-4x^2) or not.

Therefore, C is the correct option.