Answer:
The length of the arc is 2π. Therefore the correct option is 1.
Explanation:
The length of arc is
 .... (1)
.... (1)
Where, r is the radius of the circle and θ is central angle in radian.
It is given that the radius of the circle is 8 units and the central angle is 45 degrees.
Convert the central angle in radian.
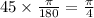
Substitute r=8 and
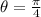 in equation (1).
in equation (1).
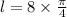

The length of the arc is 2π. Therefore the correct option is 1.